Augmented Lagrangian formulation enables topology optimization to solve mass minimization problems with over one million local von Mises stress constraints.
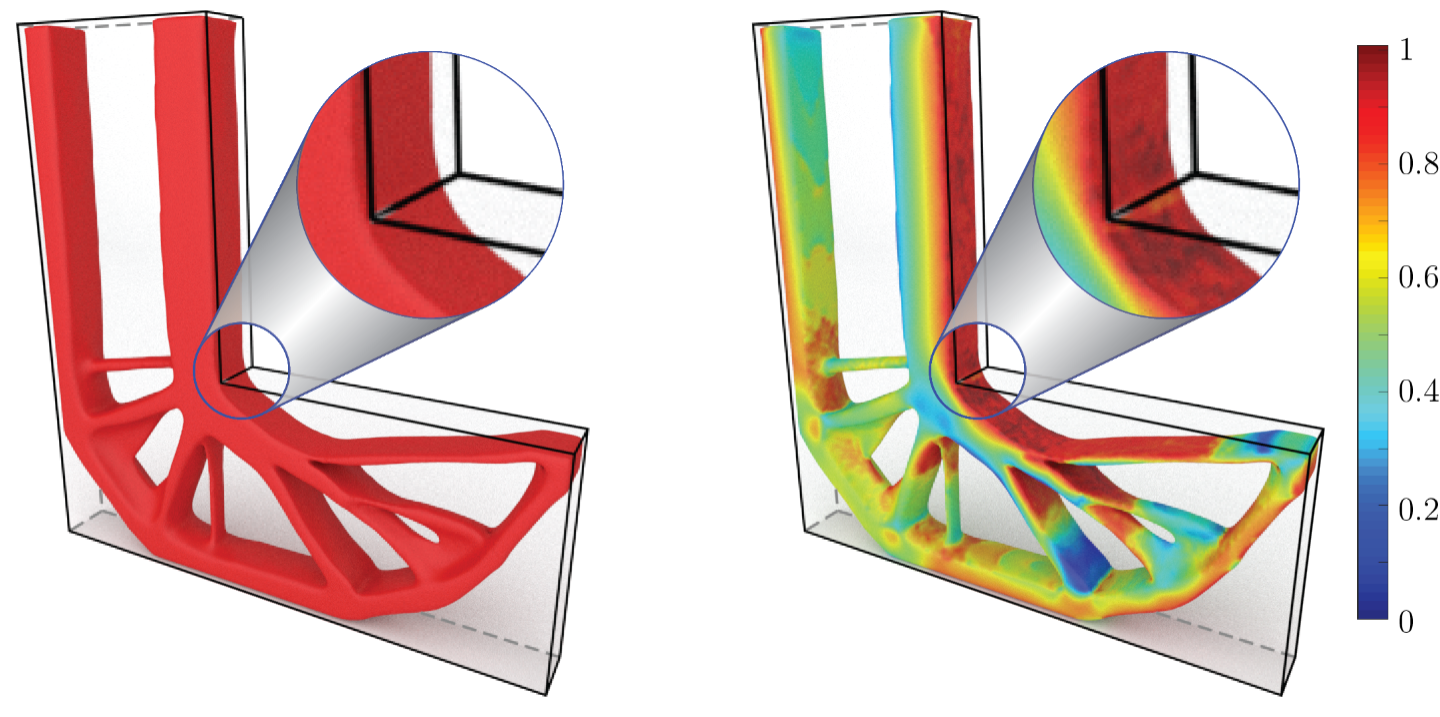
In this study we introduce a topology optimization formulation for mass minimization with local stress constraints by means of the augmented Lagrangian method.
To improve the effectiveness of the method, we modify both the penalty and objective function terms of the augmented Lagrangian function, which leads to consistent solutions under mesh refinement. Although maintaining the local nature of stress requires a large number of stress constraints, the formulation presented here requires only one adjoint vector, which results in an efficient sensitivity evaluation.
Topology optimization with local stress constraints: A stress aggregation-free approach.